QED 2-Loop

QED 2-Loop Corrections to Massive Bhabha Scattering

Elementary Particle Theory Group, Zeuthen

QED 2-Loop Corrections to Massive Bhabha Scattering

S. Actis, M. Czakon, J. Gluza, T.Riemann

This page is on our two-loop Bhabha scattering project. See also Webpage on Bhabha Scattering and Webpage on 1-Loop Corrections in the Standard Model.

Recent Papers and Talks

"Virtual Hadronic and Heavy-Fermion O(alpha**2) Corrections to Bhabha Scattering"
S. Actis, M. Czakon, J. Gluza, T. Riemann
arXiv:0807.4691, DESY-08-101, PITHA-08-18, submitted to Phys. Rev. D
NNLO loop corrections from massive flavors and from hadrons to Bhabha scattering in the limit of fixed angle and high energy for Meson Factories, LEP, ILC
Long write-up of material presented in Phys.Rev.Lett. 100 (2008) 131602
Application of dispersion technique to the Bhabha two-loop box diagrams
Comprehensive collection of different two-loop contributions with heavy fermions/hadrons
Numerics for leptons and hadrons, the latter based on H. Burkhardt's parameterization repi.f of R_had

Auxiliary files: DispersionBoxKernelMasters.m: The eight master integrals MA1 (B1) to MA8 (B8) [typo of eq.-numbering in arXiv:0807.4691], and the box kernel functions KA[s,t,z], KB[s,t,z], KC[s,t,z] expressed by them as exact functions of \epsilon, s, t, m (=m_e), z (=m_heavy^2); the expressions KAexp[s_,t_,z_], KBexp[s_,t_,z_], KCexp[s_,t_,z_] are the kernels KA, KB, KC of eqs.(71)-(73), where m_e^2 << s,t,u,z is assumed; the expressions BA, BB, BC are the analytically integrated box functions (for fermions, with R_had replaced by R_f) as published in eq.(3.20) to eq.(3.22) of Nucl.Phys. B786 (2007) 26-51; the threshold function R[u] (=R_f(u) of eq.(23) with slightly changed normalization) for fermions including the order \epsilon KernelFunctions.m: Self-energy kernel eq.(30), vertex kernel eq.(43), and three box kernels KA, KB, KC of eqs.(71)-(73); they are used for the corresponding folding in the dispersion integrals over R_had BoxFunctions.m: The three resulting box kernels I1 eq.(75) and I2 eq.(76) for the Bhabha cross-section formula after summing over all box diagrams Integrands.m: The infrared safe kernel functions F1 to F4, eqs. (88)-(91) for the Bhabha cross-section, covering box diagrams and IR-non-safe diagrams repi_1986.f: The parameterization of H. Burkhardt (1986) for R_had(s) as described in Appendix E and used for the numerics of Table III and Table IV and in Figures 9-14, 16 (called there "parameterization hadronic 1") repi_2.f: The parameterization for R_had(s) as described in items (A) to (C) in Appendix E, used for the numerics in Figures 9, 11, and 15, 16 (called there "parameterization hadronic 2") cpolylog.f: Fortran code for the evalution of complex polylogarithmic functions Li_2(z) and Li_3(z) as described in Appendix F, assuming a cut at the positive real axis starting at z=1 bhbhnnlohf: Fortran package for the evalution of the Bhabha cross section contributions from all the described contributions, see article for details.

"Virtual Hadronic and Leptonic Contributions to Bhabha Scattering"
S. Actis, M. Czakon, J. Gluza, T. Riemann
arXiv:0711.3847, Phys.Rev.Lett. 100 (2008) 131602
NNLO loop corrections from massive flavors and from hadrons to Bhabha scattering in the limit of fixed angle and high energy for Meson Factories, LEP, ILC
Application of dispersion technique to the Bhabha two-loop box diagrams
Numerics for leptons and hadrons, the latter based on H. Burkhardt's parameterization repi.f of R_had
For auxiliary files see KernelFunctions.m, BoxFunctions.m, Integrands.m, repi_1986.f,

"Fermionic NNLO contributions to Bhabha scattering"
S. Actis, M. Czakon, J. Gluza, T. Riemann
arXiv:0710.5111, Acta Phys.Polon. B38 (2007) 3517-3528
Talk given at 31st International Conference of Theoretical Physics "Matter to the Deepest: Recent Development in Physics of Fundamental Interactions", Ustron, Katowice, Poland, 5-11 Sep 2007
Transparencies of the talk: ustron07-riemann.pdf
The two-loop contributions with massive flavors to Bhabha scattering in the limit of fixed angle, high energy, and arbitrary heavy fermion mass
First application of dispersion technique to the Bhabha two-loop box diagrams
Numerics for leptons

" Two-Loop Fermionic Corrections to Massive Bhabha Scattering"
S. Actis, M. Czakon, J. Gluza, T. Riemann
arXiv:0704.2400, Nucl.Phys. B786 (2007) 26-51
The two-loop contributions with two massive flavors to Bhabha scattering in the limit of fixed angle, high energy, and intermediate heavy fermion mass
For auxiliary files see CrossSection.m, ExactResults.m, ApproxResults.m, MIs.m,

" Planar two-loop master integrals for massive Bhabha scattering: N(f)=1 and N(f)=2"
S. Actis, M. Czakon, J. Gluza, T. Riemann
hep-ph/0609051, in: Proceedings of Loops and Legs 2006, Nucl. Phys. Proc. Suppl. 160 (2006) 91-100
The master integrals are determined for the two-loop contributions with two massive flavors to Bhabha scattering in the limit of fixed angle and high energy
For auxiliary files see later, here

"The planar four-point master integrals for massive two-loop Bhabha scattering"
M. Czakon, J. Gluza, T. Riemann
Nucl.Phys. B751 (2006) 1-17 hep-ph/0604101
The complete set of planar four-point Master Integrals needed for massive Bhabha scattering in the limit of fixed angle and high energy at the two-loop level.
For auxiliary files see here

"Master integrals for massive two-loop Bhabha scattering in QED"
M. Czakon, J. Gluza, T. Riemann
Phys. Rev. D71 (2005) 073009, hep-ph/0412164
Complete lists of master integrals for Bhabha scattering with one flavor (electrons) and several flavors (e.g. electrons, muons, tauons) are given and the status of the analytical evaluation is reviewed
For auxiliary files see here

The status of the project has been described on several occasions:

LL08, "DESY Zeuthen Workshop "Loops and Legs in Quantum Field Theory", Sondershausen, Germany, April 20-25, 2008 talk by J. Gluza, "Two-loop Bhabha scattering with Nf=2" [.pdf], E-print: arXiv:0710.5111, to appear in Nucl. Phys. B (Proc. Suppl.), DESY-08-084, PITHA-08-14
LCWS 2007, "International Linear Collider Workshop (LCWS07 and ILC07)", 30 May - 3 Jun 2007, Hamburg, Germany; "Two-loop heavy fermion corrections to Bhabha scattering" S. Actis, M. Czakon, J. Gluza, T. Riemann, published in SLAC eConf C0705302, slides of SN=TeV02, see also here for slides; DESY-07-192, LCWS-2007-TEV02,
Radcor 2005, "7th International Symposium on Radiative Corrections - Application of Quantum Field Theory to Phenomenology", Shonan Village, Japan, October 2-7, 2005; "Massive two-loop Bhabha scattering", M. Czakon, J. Gluza, T. Riemann, transparencies [.ps], to appear in the proceedings
Matter To The Deepest, "XXIX International Conference of Theoretical Physics", 8-14 September 2005, Ustron, Poland; "On master integrals for massive Bhabha scattering", M. Czakon, J. Gluza, T. Riemann, transparencies [.ps], to appear in the proceedings in Acta Phys. Polonica
ACAT05, "X Int. Workshop on Advanced Computing and Analysis Techniques in Physics Research", 22-27 May 2005, Zeuthen, Germany; "Harmonic polylogarithms for massive Bhabha scattering", M. Czakon, J. Gluza, T. Riemann, hep-ph/0508212 [.ps], to appear in Nucl. Instr. Meth. A. For auxiliary files see here
Workshop on Bhabha Scattering, Univ. Karlsruhe, April 21./22., 2005; talk by T. Riemann, "Master integrals for massive 2-loop Bhabha scattering" [.ps]
LL04, "DESY Zeuthen Workshop "Loops and Legs in Quantum Field Theory", Zinnowitz, Germany, 25-30 April 2004, talk by J. Gluza, "Contributions to the 2-loop Bhabha process: new results" [.pdf]. The contribution to the proceedings by M. Czakon, J. Gluza, T. Riemann, "A complete set of scalar master integrals for massive 2-loop Bhabha scattering: where we are", hep-ph/0406203 [.ps], Nucl. Phys. B (Proc. Suppl.) B135 (204) 83, contains a short presentation of our approach in the 2-loop project.
LCWS04, "International Conference on Linear Colliders", 19-23 April 2004, Paris, France

The Feynman Diagrams

The virtual QED corrections are due to the following collection of Feynman diagrams in

Born approximation
1-loop order
2-loop order
2-loop order: set 1/8, set 2/8, set 3/8, set 4/8, set 5/8, set 6/8, set 7/8, set 8/8
2-loop order, 1PI diagrams only

To be definite, we assume three generations of leptons. Further, we do not show the Feynman diagrams for the renormalization of external legs.

The Master Integrals

Such a calculation contains several key elements. The corrections may be written in terms of some set of scalar integrals, which are then subject of reliable analytical and/or numerical evaluation. A non-trivial problem is the determination of a sufficiently small, but complete set of scalar integrals, the so-called master integrals.
There are only few different topologies of diagrams to be calculated, they include

self energies: 4 diagrams, 6 master integrals
vertices: 5 diagrams, 19 master integrals
boxes: 6 diagrams, 33 master integrals
1-loop: 6 master integrals of different type

Self-energies

There are contributions from four 2-loop self-energies.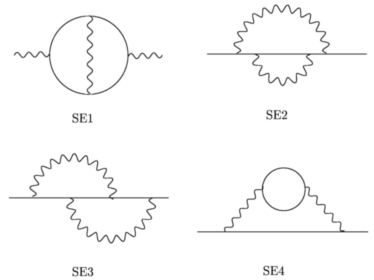

Diagram SE1 is needed for the evaluation of the Bhabha cross section, and SE2 to SE4 are needed for the renormalization of external fermion legs:

SE3lx,SE5lx: A complete set of six 2-loop self energy master integrals, which is sufficient to calculate all the 2-loop Feynman diagrams

Vertices

There are contributions from five 2-loop vertices: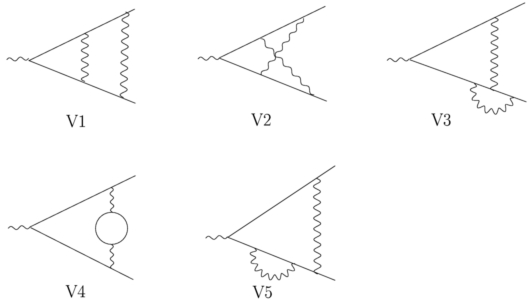

A complete set of nineteen 2-loop vertex master integrals, which is sufficient to calculate all the vertex and box Feynman diagrams:

V6l4mx: The three 2-loop vertex MIs with six internal lines
V5l2mx,V5l3mx: The six 2-loop vertex MIs with five internal lines
V4l1mx...V4l4mx: The ten 2-loop vertex MIs with four internal lines

Boxes

There are contributions from six 2-loop boxes: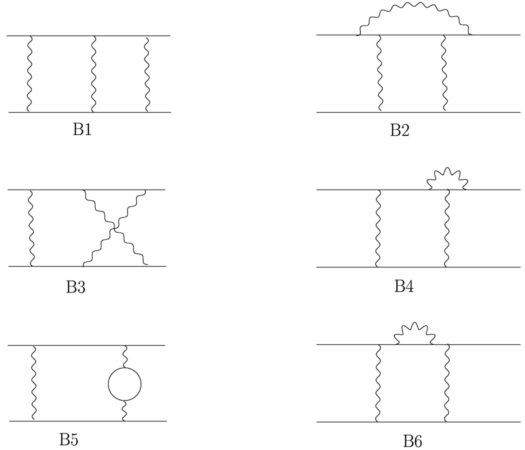

A complete set of thirty three 2-loop box master integrals, which is sufficient to calculate all the box Feynman diagrams:

B7l4mx: The nine 2-loop box MIs with seven internal lines
B6l3mx: The ten 2-loop box MIs with six internal lines
B5l2mx: Eight of the forteen 2-loop box MIs with five internal lines
B5l3mx,B5l4mx: Six of the forteen 2-loop box MIs with five internal lines

1-loop masters

There are six 1-loop master integrals needed for the evaluation of the 2-loop diagrams: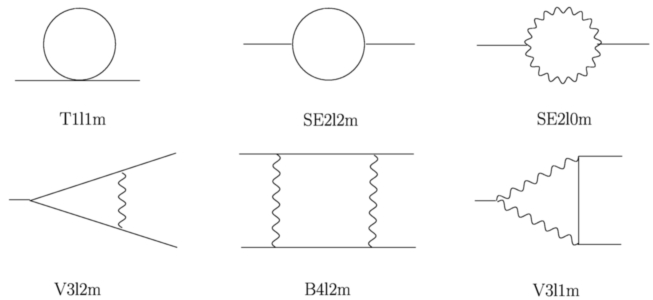

Who needs whom?

For the calculation of a certain diagram out of the set of diagrams [SE1,..Se4,V1,..V5,B1,..B6] only a certain subset of master integrals will be needed. In the following table, we indicate the number of (2-loop + 1-loop) master integrals needed to calculate the 2-loop vertex diagrams V1 to V5 and box diagrams B1 to B6:

masters overview [.pdf],

In the next three tables, a '+' means that the corresponding master integral contributes to the diagram. Stars denote 1-loop MIs, and the terminus 'oms' means on-mass-shell. For the 2-loop master integrals, we indicate also the reference if the master is known analytically (status of June 2004).

2LSE: list of tadpole and self energy master integrals needed for each of the 2-loop self energy diagrams
2LVB: list of tadpole, self energy and vertex master integrals needed for each of the 2-loop vertex and box diagrams in a model with flavor number Nf=1.
V4 and B5 (and the corresponding masters) have also to be determined for Nf>1 cases.
2LB: list of box master integrals needed for each of the 2-loop box diagrams.

Explicit analytical expressions for master integrals

The file

MastersBhabha.m

contains the analytical expressions for all the self energy and vertex master integrals needed, and also for few of the box master integrals, which we calculated so far.
The analytical expressions are numerically checked using sector decomposition as proposed in [11,12]. The master integrals are identified with the names of the masters as given in the figures accessible above on this page.

Comparisons

Our set of master integrals includes also masters which were calculated earlier by other groups. For references we refer to the tables given above: 2LSE, 2LVB, 2LB. In comparisons, one has to take into account the different normalizations of the master integrals as well as the different definitions of their series expansions in (d-4).

Our conventions
Some other conventions

For some time there was a disagreement of the following master integrals in MastersBhabha.m with expressions published earlier (see also hep-ph/0406203 [.ps]):

SE3l1m, SE3l2mN, V4l3md, V4l4m, V4l4mN, V6l4m1, B4l2m, B5l4m, B5l4mN

More details: see here. For the references [3] and [9] Errata have been prepared by the authors and FORM files with analytical expressions with the master integrals of [3] and of [9] habe been made available at the Bhabha scattering web pages at Freiburg University.

References

The following articles have been quoted in this webpage and in the tables:

M. Czakon, J. Gluza and T. Riemann, hep-ph/0406203 v2, Contrib. to the Proceedings of the Workshop ``Loops and Legs in Quantum Field Theory'', April 25-30, 2004, Zinnowitz, Germany, to appear in Nucl. Phys. (Proc. Suppl.) B135 (204) 83.
R. Bonciani, P. Mastrolia and E. Remiddi, Nucl. Phys. B690 (2004) 138, hep-ph/0311145 v2 (20 April 2004).
R. Bonciani, P. Mastrolia and E. Remiddi, Nucl. Phys. B661 (2003) 289, hep-ph/0301170 v4 (25 June 2004).
M. Argeri, P. Mastrolia and E. Remiddi, Nucl. Phys. B631 (2002) 388, hep-ph/0202123.
J. Fleischer, A.V. Kotikov and O.L. Veretin, Nucl. Phys. B547 (1999) 343, hep-ph/9808242.
A.I. Davydychev and M.Y. Kalmykov, (2003), hep-th/0303162.
V.A. Smirnov, Phys. Lett. B524 (2002) 129, hep-ph/0111160.
G. Heinrich and V.A. Smirnov, (2004), hep-ph/0406053.
R. Bonciani et al., Nucl. Phys. B681 (2004) 261, hep-ph/0310333 v3 (25 June 2004).
J. Fleischer and M. Kalmykov, Comput. Phys. Commun. 128 (2000) 531, hep-ph/9907431.
T. Binoth and G. Heinrich, Nucl. Phys. B585 (2000) 741, hep-ph/0004013.
T. Binoth and G. Heinrich, Nucl. Phys. B680 (2004) 375, hep-ph/0305234.

Additional information related to hep-ph/0412164:

In M. Czakon, J. Gluza, T. Riemann, "Master integrals for massive two-loop Bhabha scattering in QED" we refer to:

MastersBhabha.m: A mathematica file with master integrals (so far not updated compared to hep-ph/0406203 by the additional masters given in hep-ph/0412164)
Substitutions_V5l2m2.m: Some algebraic substitutions for the evaluation of scalar integrals of prototype V5l2m2 in terms of master integrals, which have been used in hep-ph/0412164, but are not given explicitely there.
HPL4.m: A mathematica file with Harmonic Polylogarithms up to weight 4

go back to hep-ph/0412164

Additional information related to hep-ph/0508212:

In M. Czakon, J. Gluza, T. Riemann, "Harmonic polylogarithms for massive Bhabha scattering" we refer to:

GPL.m: A mathematica file with GPLs (generalized harmonic polylogarithms) up to weight 4
GPLtransf.m: A mathematica file with relations between GPLs with interchanged arguments x and y
GPLconf.m: A mathematica file with relations between GPLs with arguments x,y and x',y'; two different sets of conformal variables for s and t

go back to hep-ph/0508212

Additional information related to hep-ph/0604101:

In M. Czakon, J. Gluza, T. Riemann, "The planar four-point master integrals for massive Bhabha scattering" we refer in Section 2 to the following files:

BoxMIsExpanded.m: A mathematica file with the planar master integrals in the limit of high energy and fixed scattering angle, given both for the t-channel and the s-channel.
Dots_Numerators.nb.ps: A notebook copy with the algebraic relations between the masters with dots of the topology B5l2m3 as given in our original table of masters and the alternative masters with numerators as calculated in the article. Similar relations have also been derived for all the other cases.
FORM output files, generated by Stefano Actis, with the information about the Feynman integrals needed for the calculation of the virtual two-loop corrections to the differential Bhabha cross-section from the double-box topologies:
topology B1,
topology B2,
topology B3,
topology B4,
topology B5,
topology B5nf,
topology B6.

go back to hep-ph/0604101